Algemene mechanische wetten.

Op een fiets wordt energie uit de trapkracht van de fietser omgezet in een voorwaartse beweging. Om de werking van de diverse onderdelen in de fiets te kunnen begrijpen is het handig om enige regels uit de algemene mechanische wetten te kennen en te begrijpen. Ze zijn echt niet zo moeilijk.

Het belangrijkste begrip in de mechanica is de Kracht.

Als op een voorwerp een kracht wordt uitgeoefend
kan dit drie effecten tot gevolg hebben:

• of het voorwerp gaat versnellen
  – of het voorwerp blijft stil liggen of staan
• of het voorwerp gaat met constante snelheid bewegen.

Als een voorwerp niet gaat versnellen moet de omgeving een reactiekracht uitoefenen op het voorwerp.

Voor voorwerpen die niet in rust zijn geldt:

F = m x a

waarbij:

F = de kracht in N
m = de massa in kg
a = de versnelling in m/s

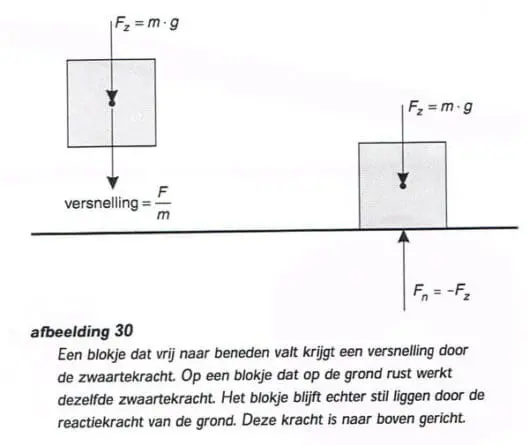
Op een voorwerp dat vrij naar beneden valt werkt alleen de zwaartekracht. Hierdoor zal het voorwerp een versnelling krijgen en steeds sneller bewegen. Als er wel een reactiekracht werkt dan heeft de reactiekracht een waarde van -F. De wet die hier geldt is: actie is reactie.

Voor voorwerpen die in rust zijn geldt:

F actie = F reactie

Op een voorwerp dat op de grond ligt werkt de zwaartekracht. Het voorwerp blijft stil liggen omdat de grond ook een kracht uitoefent ter waarde van –F zwaartekracht. Zie afbeelding 30.

Een tweede belangrijk begrip in de mechanica is het Moment. Als op een afstand van een voorwerp een kracht wordt uitgeoefend, oefent die kracht een moment uit op dat voorwerp ter waarde van de kracht x de afstand. Meestal wordt die afstand arm of hefboom genoemd.

De formule wordt:

M = F x 1

Waarbij:

M = het moment in Nm
F = de kracht in N
1 = de afstand in m.

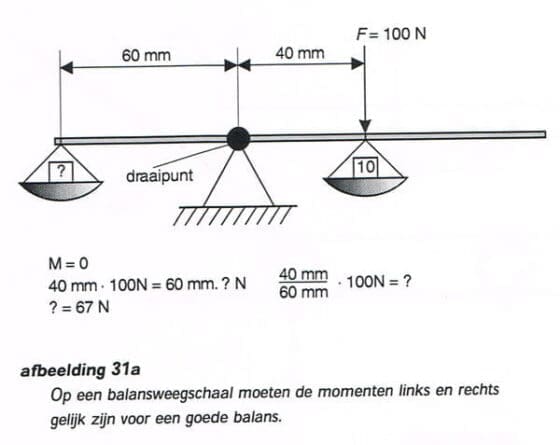
Voor momenten geldt hetzelfde als voor krachten. Door momenten kan een voorwerp zich echter niet verplaatsen, maar draait het om zijn as. Als op een voorwerp een moment wordt uitgeoefend kan dat versneld gaan draaien, het blijft stil staan, of het gaat met constante snelheid draaien. Als het blijft stilstaan moet er een reactiemoment op dat voorwerp werken. Het reactiemoment heeft dezelfde grootte maar een tegengestelde draairichting. Bij een balansweegschaal is goed te zien dat de momenten in evenwicht moeten zijn.

Als links van het draaipunt van de balans een massa geplaatst wordt van 10 kg op een afstand van 10 cm en je plaatst rechts van het draaipunt een massa van 5 kg op een afstand van 20 cm dan is de weegschaal in ‘balans’.

Er geldt:

M actie = M reactie

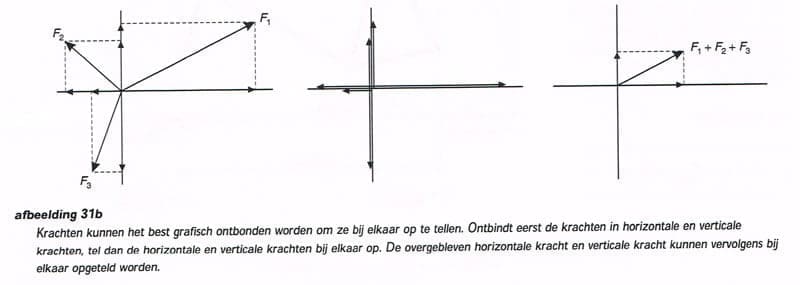
Krachten kunnen ontbonden worden in horizontale krachten en verticale krachten. Dit is handig omdat hiermee gekeken kan worden of er horizontaal en/of verticaal evenwicht is. De makkelijkste manier om krachten te ontbinden is grafisch. Krachten die dezelfde richting hebben en dezelfde kant op wijzen kunnen bij elkaar opgeteld worden, grafisch weergegeven worden ze dan twee keer zo lang. Krachten die dezelfde richting hebben maar de tegengestelde kant op wijzen kunnen van elkaar afgetrokken worden. Als de som van de krachten 0 is zal een voorwerp in rust blijven of met constante snelheid blijven bewegen. Als de som van de krachten niet 0 is zal het voorwerp gaan bewegen in de richting waar de kracht naar wijst.

Voor de waarde van de kracht geldt:

F horizontaal = F x cos (?)
F verticaal = F x sin (?)

waarbij:

(?) = de hoek die de kracht maakt met de horizontale lijn.

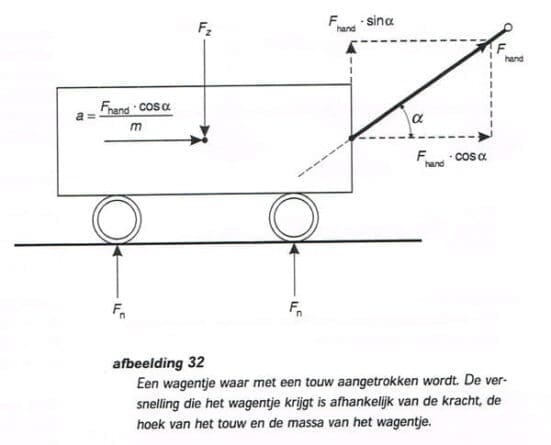
Een wagentje waar bijvoorbeeld met een touw aan getrokken wordt zal in horizontale richting een versnelling krijgen. Zie afbeelding 32.

De waarde is:

m x a = F hand x cos (?)

In verticale richting is er evenwicht. De reactiekracht van de grond op het wagentje is:

F reactie = F hand X Sin (?) – F zwaartekracht

Een voorwerp waar een kracht of moment op uitgeoefend wordt zal met constante snelheid bewegen of stil blijven staan als de krachten in horizontale en verticale richting gelijk zijn en als de momenten gelijk zijn. Zie afbeelding 31. Algemeen wordt dit geformuleerd als: de som van de krachten en momenten op een voorwerp in rust is gelijk aan nul.

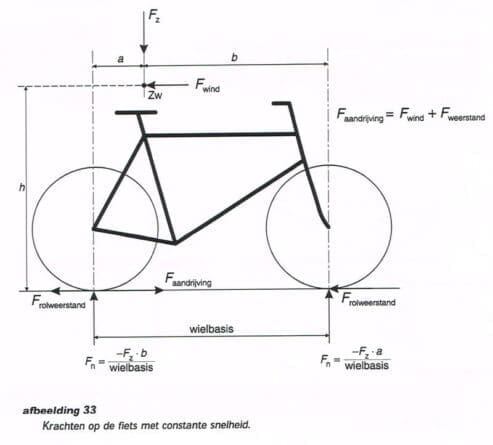
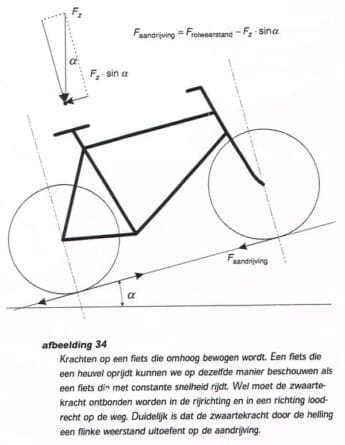
Met dit gegeven kunnen bijvoorbeeld de krachten op een fiets bepaald worden. Als een fiets met constante snelheid rijdt, werken daar de volgende krachten op: de zwaartekracht, de weerstand door de wind, de aandrijfkracht op het achterwiel, de normaalkrachten op de wielen en de rolweerstand van de wielen (een kracht die een beweging tegengaat wordt weerstand genoemd). Zie afbeelding 33. Als de rolweerstand, rijwind, plek van het zwaartepunt en massa bekend zijn, kunnen de aandrijfkracht en de reactiekracht berekend worden.

De krachten in horizontale richting zijn in evenwicht. Daarmee wordt F achterwiel = F rijwind + F rolweerstand

De krachten in verticale richting zijn in evenwicht. Daarmee wordt F achterwiel + F voorwiel = F zwaartekracht

Helaas is hiermee de reactiekracht op de voor- en achterwielen nog niet uit te rekenen. Daarvoor moet ook de som van momenten gelijk zijn. Het draaipunt waar we de momenten om uitrekenen moet slim gekozen worden. Omdat de krachten bij het achterwiel en voorwiel beide nog onbekend zijn is het handig om de momenten om het voor- of achterwiel uit te rekenen.

Als we het om het achterwiel doen, wordt de vergelijking:

F voorwiel x wielbasis + F rijwind x h – F zwaartekracht x a = 0

Meestal is de winddruk te verwaarlozen zodat de reactiekracht op het voorwiel –Fz x a/wielbasis bedraagt en op het achterwiel –Fz x b/wielbasis. Bij een fiets gaat het niet alleen om krachten en momenten. Het gaat ook om verplaatsingen. Om een kracht over een afstand te verplaatsen moet er arbeid verricht worden. Als tegen een voorwerp aangeduwd wordt zonder dat dat voorwerp in beweging komt, is er geen arbeid verricht. De arbeid is kracht x de afgelegde weg. Blijft het stil liggen, dan is er geen afgelegde weg, dus is kracht maal weg gelijk aan nul.

Er geldt:

W = F x s
W = arbeid in Nm
F = kracht in N
S = afgelegde weg in m

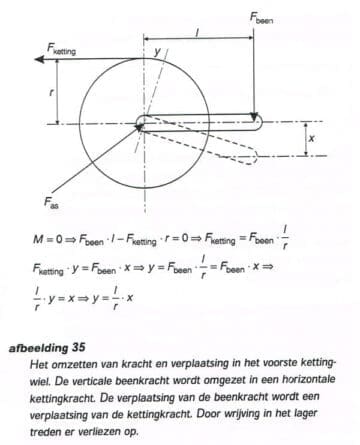
De fiets is te beschouwen als een mechanische omzetter of versterker. Zie afbeelding 35. Een mechanische omzetter is een mechanisme dat een ingaande kracht en verplaatsing omzet in een uitgaande kracht en verplaatsing en de richting van de kracht kan veranderen. Zo zet het voorste kettingblad de verticale beenkracht op de crank om in een horizontale trekkracht in de ketting. De arbeid die in een mechanische versterker gestopt wordt moet er ook weer uitkomen.

Er geldt:

F in x l in = F uit x l uit
F in = de kracht die in de versterker wordt gestopt in N
l in = de verplaatsing van de kracht die in de versterker wordt gestopt in m
F uit = de kracht die uit de versterker komt in N
l uit = de verplaatsing uit de versterker in m.

 

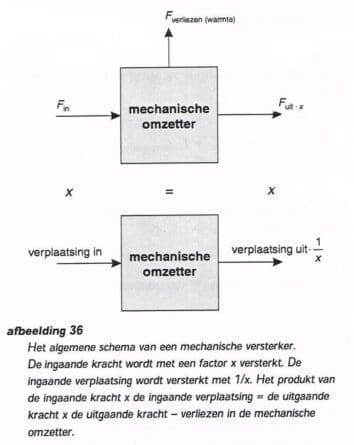
De fiets bestaat uit een groot aantal mechanische omzetters. Zie afbeelding 36.

Het wiel, de ketting, de tandwielen, de remgreep, de kabels en de versnellingsnaaf zijn allemaal als mechanische omzetters te beschouwen. Bij het bestuderen van de diverse onderdelen op de fiets is het handig om goed te kijken wat er met de krachten en verplaatsingen gebeurt en waar er mogelijk verliezen optreden. Zo is direct te zien dat met schroefdraad een grote kracht is uit te oefenen.

Immers, een grote verplaatsing van de kracht op de sleutel leidt maar tot een zeer kleine verplaatsing van de bout of moer. Aangezien het product van de ingaande kracht en verplaatsing gelijk moet zijn aan de uitgaande kracht en verplaatsing moet de uitgaande kracht groot zijn.